Thompson et al. (2003): Circular phosphenes

This example shows how to use the Thompson2003Model.

The model introduced in [Thompson2003] assumes that electrical stimulation leads to circular percepts with discrete gray levels. The model also allows for a fraction of phosphenes to be omitted at random (dropout rate).

The model can be loaded as follows (using 10% dropout rate):

import matplotlib.pyplot as plt
import numpy as np
import pulse2percept as p2p
model = p2p.models.Thompson2003Model(xystep=0.2, dropout=0.1)
model.build()

Thompson2003Model(dropout=0.1, engine=None,
                  grid_type='rectangular', n_gray=None,
                  n_jobs=1, n_threads=2, ndim=[2],
                  noise=None, radius=None,
                  scheduler='threading',
                  spatial=Thompson2003Spatial,
                  temporal=None, thresh_percept=0,
                  verbose=True,
                  vfmap=Curcio1990Map(ndim=2),
                  xrange=(-15, 15), xystep=0.2,
                  yrange=(-15, 15))

After building the model, we are ready to predict percepts. Here we will use an ArgusII implant.

One way to assign a stimulus is to pass a NumPy array with the same number of elements as there are electrodes in the array (i.e., 60). Choosing values from np.arange(60) will assign a different number to every electrode. We should thus expect to see 60 circular phosphenes that get gradually brighter from one electrode to the next:

implant = p2p.implants.ArgusII(stim=np.arange(60))
percept = model.predict_percept(implant)
percept.plot()

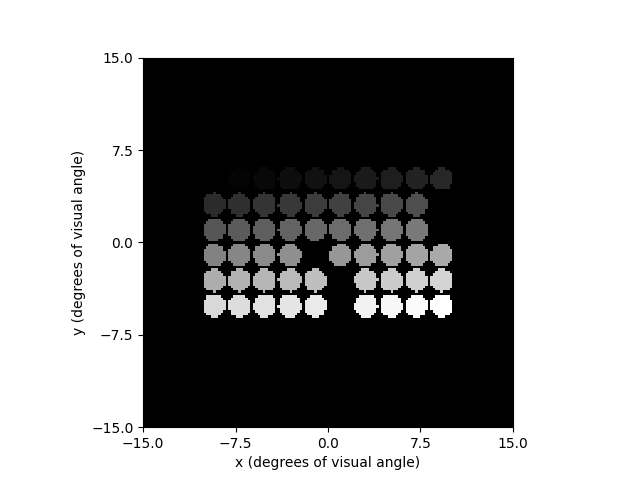
<Axes: xlabel='x (degrees of visual angle)', ylabel='y (degrees of visual angle)'>

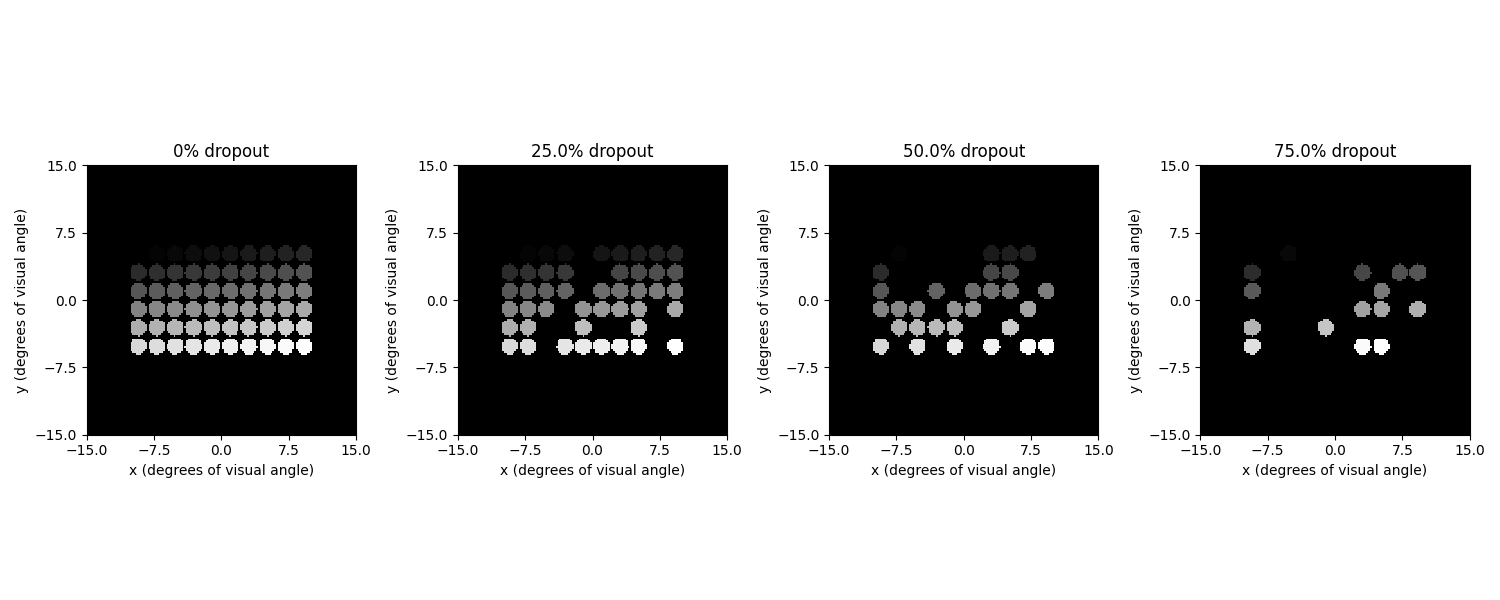
Setting a nonzero dropout rate will randomly choose a fraction of phosphenes to disappear:

fig, axes = plt.subplots(ncols=4, figsize=(15, 6))
for ax, drop in zip(axes, [0, 0.25, 0.5, 0.75]):
    model.build(dropout=drop)
    model.predict_percept(implant).plot(ax=ax)
    ax.set_title(f"{100*drop}% dropout")
fig.tight_layout()

Finally, the model can also be applied to VideoStimulus objects, where every frame of the video will be encoded with circular phosphenes and a given dropout rate:

implant.stim = p2p.stimuli.BostonTrain()
model.build(dropout=0.2)
model.predict_percept(implant).play()

Once Loop Reflect